
Сьогоднішні підходи до надання медичної допомоги та філософія медицини загалом доволі сильно відрізняються від тих, що панували ще 100 років тому.
Одна лише згадка про речі, які ще на початку минулого сторіччя вважались нормальними та широко застосовувались (використання ртуті для лікування сифілісу, чи кокаїну для зменшення зубного болю), сьогодні в багатьох може викликати лише іронічну посмішку та радість від того, що такі підходи вже давно пішли в минуле, вже давно не використовуються та більше ніколи використовуватись не будуть (мабуть).
О дивний світ новий доказової медицини!
Завдяки кардинальній зміні підходів до лікування та впровадженню доказової медицини, тепер людство знає, що артеріальний тиск необхідно підтримувати на рівні нижче 120/80 мм. рт. ст., глюкозу крові нижче 5.6 ммоль/л, мати хоча б 150 хвилин помірної фізичної активності на тиждень та багато інших речей, не кажучи вже про те, що ртуть не дуже підходить для лікування інфекційних захворювань, а кокаїн краще не використовувати для зменшення зубного болю (особливо у дітей).
Звичайно, впровадження та застосування доказової медицини має величезні переваги, однак, має й свої недоліки, про які ми вже згадували в статті “Що таке доказова медицина насправді”.
Доказова медицина побудована, що очевидно, на доказах, які отримують в ході досліджень. Кожне нормальне дослідження так чи інакше будується таким чином, щоб отримати певні дані, які потім аналізують, використовуючи інструменти біостатистики, та роблять відповідні висновки.
І якщо з розумінням концепцій збору даних, тобто з розробкою дизайну дослідження, проблем не виникає, адже інтуїтивно зрозуміло, що подвійне сліпе рандомізоване плацебо контрольоване дослідження за участі 15000 осіб дасть більш точну відповідь на певне запитання, ніж ретроспективний аналіз даних 100 осіб, то з інтерпретацією результатів досліджень у деяких можуть виникнути проблеми.
Risk difference, risk ratio, odds ratio, hazard ratio, довірчі інтервали, значення p, а ззаду ще тихенько підкрадається регресійний аналіз…
Починає складатись враження, що медицина потроху переростає в математику та, зокрема, статистику, без розуміння основ якої не можна повністю осягнути й пізнати медицину, а творчий та особистий підхід до лікування кожного окремого пацієнта залишився десь в минулому разом з втиранням в дитячі ясна кокаїну. Можливо, це твердження є доволі суперечливим, а ars medicina й досі бовваніє над кожним закладом охорони здоров’я, однак, беззаперечним є той факт, що математика й статистика вже давно посіли в медицині одну з провідних ролей (якщо не провідну).
Тож є доволі очевидним, що без розуміння основ біостатистики лікарю буде доволі важко зрозуміти, чому одним з критеріїв встановлення діагнозу цукрового діабету другого типу є рівень глікованого гемоглобіну саме 6,5% і вище, чому безсимптомну бактеріурію не варто лікувати у жінок без факторів ризику, чим керуються асоціації, коли розробляють клінічні настанови, та багато-багато інших речей.
Отже, нас чекає ще один захопливий (сподіваємось) статистичний дайвінг, після якого Ви будете мати непогане загальне уявлення про основи біостатистики, базові розрахунки, що виконуються в ході досліджень, та зможете інтерпретувати їх результати (сподіваємось).
Готові? Пірнаємо.
Дисклеймер: ми вже намагались трошки розібратись в біостатистиці в статті під назвою “Що таке доказова медицина насправді”, в якій зокрема торкнулись розуміння та інтерпретації довірчого інтервалу, саме тому дайвінг вже не перший; тож щоб краще себе підготувати до цього, можливо, глибшого занурення, рекомендуємо спочатку ознайомитись з попередньою статтею, а вже потім переходити до цієї. Рішення, звичайно, завжди залишається за Вами.
Спочатку давайте розберемось з усіма оцими ratio (відношеннями), які доволі часто зустрічаються в дослідженнях, розраховуються за схожим принципом, однак, інтерпретуються по-різному.
Значення будуть подані англійською мовою, щоб, по-перше, спростити орієнтування в англомовних джерелах та, по-друге, щоб уникнути плутанини з термінами “risk ratio” та “hazard ratio”, які є різними показниками, однак, обидва з яких іноді перекладаються як “відношення ризиків” (див. нижче).
Уявімо (подальші значення будуть виключно уявними, взяти автором “з голови” з метою пояснення на простому та зрозумілому прикладі), що вам необхідно визначити, яким чином стать впливає на вагу людини. Ви взяли 550 осіб (зробили вибірку) та поділили їх на групи згідно ваги та статі й отримали дані, які можна представити у вигляді наступної таблиці:
| Жінки | Чоловіки | ||
| Вага ≤65 кг | 194 | 166 | 360 |
| Вага >65 кг | 76 | 144 | 220 |
| 270 | 280 | 550 |
А тепер слідкуйте за руками. Фокус ну дуууже нескладний. Ви зможете повторити його самі, навіть не маючи під рукою комп’ютера та відповідного програмного забезречення.
Тож, який відсоток (пропорція – proportion – p̂) жінок з вибірки мають вагу понад 65 кг? Рахуємо:
p̂(жінки) = 76/270 = 0.28 = 28%
А серед чоловіків?
p̂(чоловіки)= 144/280 = 0.51 = 51%
Тепер, лише на основі цих даних ми можемо розрахувати аж 3 основні показники: risk difference, risk ratio та odds ratio.
1. Risk difference: 0.28 - 0.51 = -0.23(23%).
Інтерпретація: жінки мають на 23% менший абсолютний “ризик” мати вагу понад 65 кг, порівнюючи з чоловіками.
2. Risk ratio: 0.28/0.51 = 0.55.
Інтерпретація: жінки мають на 45% (1 - 0.55 = 0.45 = 45%) менший відносний ризик мати вагу понад 65 кг, порівнюючи з чоловіками.
Risk difference частіше застосовують, коли мова йде про велику сукупність. Наприклад, на основі наших уявних даних можна зробити припущення, що серед 1000 жінок та 1000 чоловіків, жінок з вагою понад 65 кг буде на 230 менше, ніж чоловіків. Risk ratio здебільшого стосується кожної особи окремо. Наприклад, знову ж таки на основі наших уявних даних, кожна жінка в середньому має на 45% менший шанс мати вагу понад 65 кг.
3. Odds ratio.
Odds ratio можна перекласти як “відношення шансів”. Шанс розраховується за формулою:
p̂/1-p̂
Тобто для жінок шанс мати вагу понад 65 кг складає:
Odds(жінки) = 0.28/1-0.28 = 0.28/0.72 = 0.39
Для чоловіків:
Odds(чоловіки) = 0.51/1-0.51 = 0.51/0.49 = 1.04
Отже, відношення шансів розраховується…. Так, Ви й самі здогадались:
Odds ratio(жінки/чоловіки) = 0.39/1.04 = 0.38
Інтерпретація: жінки мають на 62% (1-0.38=0.62=62%) менший шанс мати вагу понад 65 кг, порівнюючи з чоловіками.
4. Hazard ratio (або Incidence rate ratio, це синоніми). Для пояснення й інтерпретації цього показника наш приклад із зростом не підійде, адже Hazard ratio розраховується у випадках, коли є дані, пов’язані з часом (time-to-event data).
Наприклад, ми маємо дані щодо кількості випадків аутоімунного гепатиту серед чоловіків та жінок в певній країні за певний проміжок часу.
Уявімо, що для жінок цей показник становить 1653 випадки на 6,451,573 людино-років, а для чоловіків 1187 випадки на 5,929,987 людино років.
Отже, для жінок частота (Incidence rate, IR) захворювань на аутоімунний гепатит складає:
IR(жінки) = 1653/6.451.573 = 0.00026 випадків на людино-рік
Для чоловіків:
IR(чоловіки) = 1187/5,929,987 = 0.0002 випадків на людино-рік
Тож Hazard ratio для жінок буде становити:
IRR(жінки/чоловіки) = 0.00026/0.0002 = 1.3
Інтерпретація: жінки мають на 30% більший ризик розвитку аутоімунного гепатиту протягом певного проміжку часу, порівнюючи з чоловіками (числа та розрахунки уявні, однак, аутоімунний гепатит дійсно частіше трапляється у жінок).
Математична цікавинка: якщо ми порахуємо не зменшення відносного ризику (див. Risk ratio вище), а збільшення (тобто в чисельнуку буде p̂(чоловіча стать)), то отримаємо наступне значення: 0.51/0.28 = 1.82 = 182%.
Отже, жінки мають на 45% (1 - 0.55 = 0.45 = 45%) МЕНШИЙ відносний ризик мати вагу понад 65 кг, порівнюючи чоловіками, однак, чоловіки мають на 82% БІЛЬШИЙ відносний ризик мати вагу понад 65 кг. Така різниця пояснюється тим, що якщо ризик зменшується, то значення завжди лежать між 0 та 1, а якщо збільшується, то між 1 та нескінченністю. Тому деякі розрахунки для відношень (зокрема, довірчого інтервалу) проводять у натуральних логарифмах, які потім підлягають експонентуванню.
Кінець математичної цікавинки.
З основними показниками розібрались. Як бачимо, розрахунки доволі прості та можуть бути виконані лише за допомогою калькулятора, папірця та ручки (якщо ви полюбляєте екстрим, то можете рахувати навіть без калькулятора!).
Однак, повертаючись до прикладу з вагою, залишилось ще одне питання: чи можемо ми екстраполювати дані, отримані на основі вибірки з 550 людей, на всю популяцію? Тобто чи можемо ми, наприклад, дізнатись, яким буде показник Risk Ratio для всієї популяції, маючи дані лише 550 осіб?
Так, можемо, розрахувавши довірчий інтервал -- Confidence Interval (тема, якої ми торкались у статті “Що таке доказова медицина насправді, з якою ще раз рекомендуємо ознайомитись перед тим, як йти далі).
Наприклад, нас цікавить яким буде показник Risk Ratio для всіх жінок та чоловіків (для всієї популяції). Нагадаємо, що для нашої вибірки RR становить 0.55. Аби дізнатись значення для популяції, ми розрахуємо довірчий інтервал. Не будемо перевантажувати вас формулами та розрахунками (розрахунки не дуже важкі, проте, довірчий інтервал для RR розраховується з переведенням чисел в натуральний логарифм ln(RR)).
Отже, маємо наступні дані для нашого виключно уявного випадку:
RR: 0.55 (95% CI від 0.48 до 0.67)
Якби ми кожного разу робили нову вибірку з 550 осіб та рахували 95% довірчий інтервал знову й знову до нескінченності, то до складу 95% таких інтервалів буде входити істинне значення для популяції. Таким чином, якщо розрахований нами інтервал “попав”, то зменшення відносного ризику мати вагу понад 65 кг для жінок, порівнюючи з чоловіками, для всієї популяції лежить десь між 33% та 52%, за умови, що інтервал “попав” (залишається ще 5% вірогідності, що до складу нашого довірчого інтервалу не входить істинне значення, яке може становити, наприклад, 20% чи 85%, та ніхто ніколи цього не дізнається – повертаємось до “Що таке доказова медицина насправді”).
Але звідки нам відомо, що саме 95% інтервалів таки попадуть і будуть мати у складі істинне значення для популяції (тобто показник, який би ми отримали, якби дійсно мали дані усієї популяції)?
Ще трошки вашої уваги, адже ми якраз дістались до одного з основних постулатів біостатистики – центральної граничної теореми.
Центральна гранична теорема свідчить, що якщо взяти всі можливі вибірки розміром n з однієї популяції та розраховувати певний показник (наприклад, середнє, пропорцію і тому подібне) для кожної вибірки, то врешті-решт розраховані показники будуть мати нормальний розподіл.
Ідеальний нормальний розподіл виглядає так:
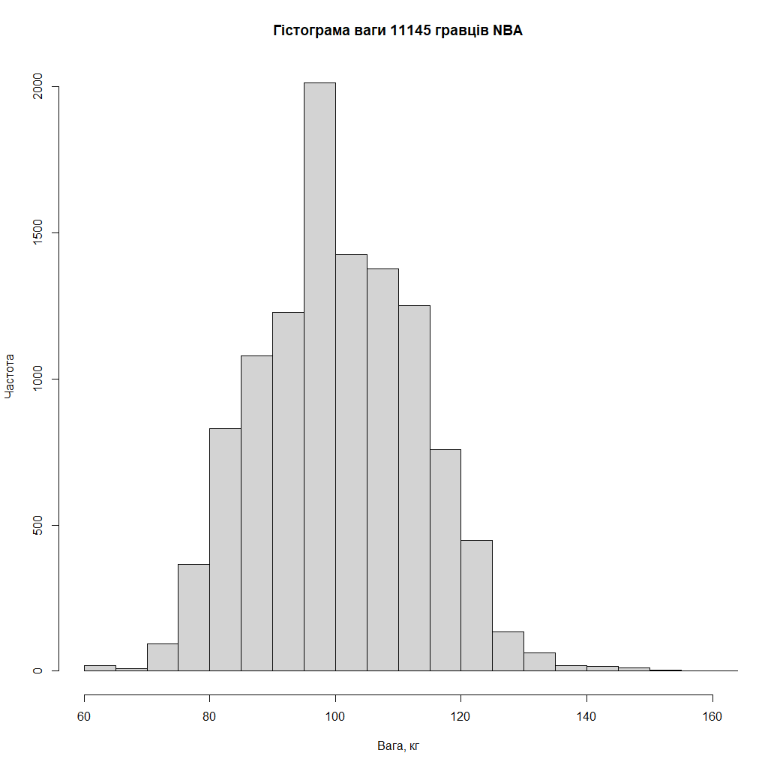
Розберемо на прикладі. Для цього з сайту Kaggle завантажимо базу даних з вагою 11145 гравців NBA – в даному випадку це буде популяція гравців NBA (логічно). Гістограма розподілу ваги всіх гравців виглядає так:
Тепер будемо робити вибірку, скажімо з 50 гравців, та розраховувати середнє. Результати розподіл середніх значень ваги для 25 вибірок з 50 гравців, для 75 вибірок, 1000 вибірок та 2500 вибірок представлені на рисунках нижче (червона лінія – середнє значення з середніх).
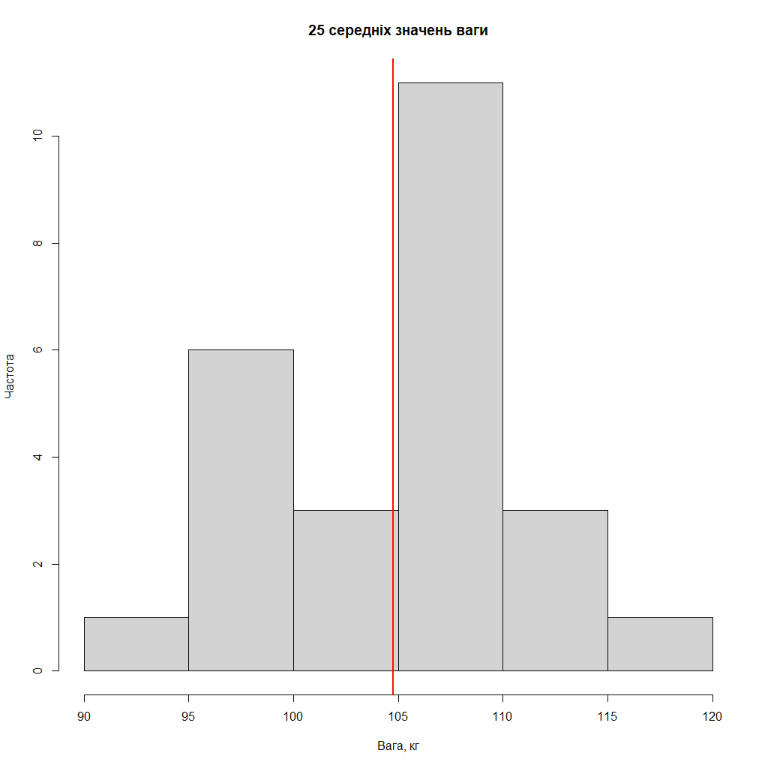
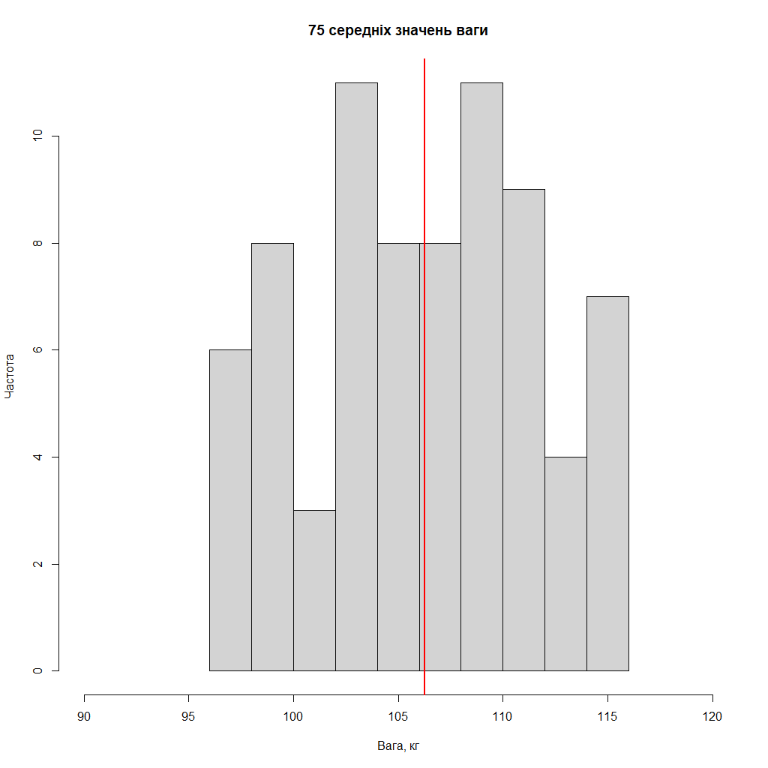
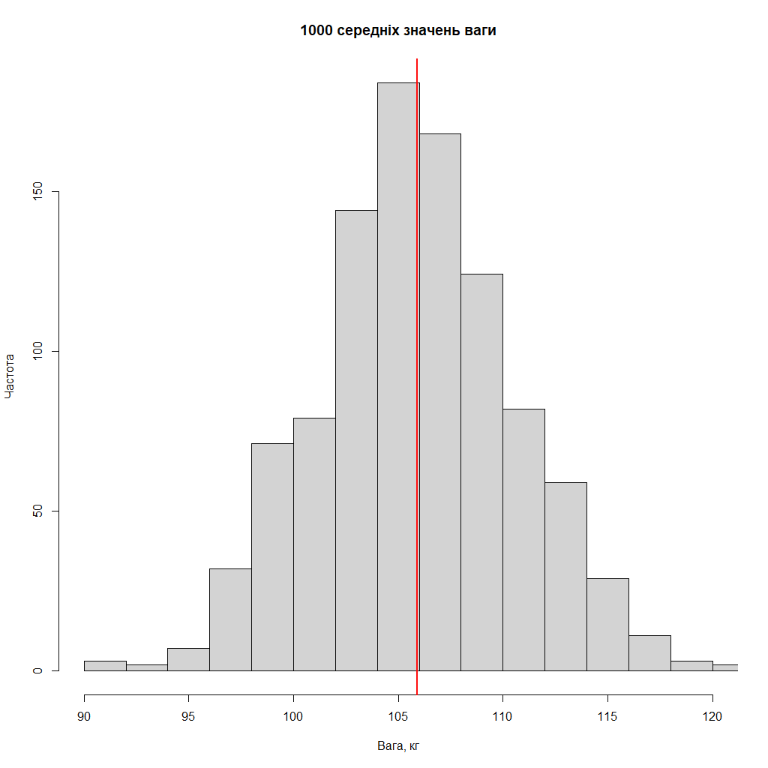
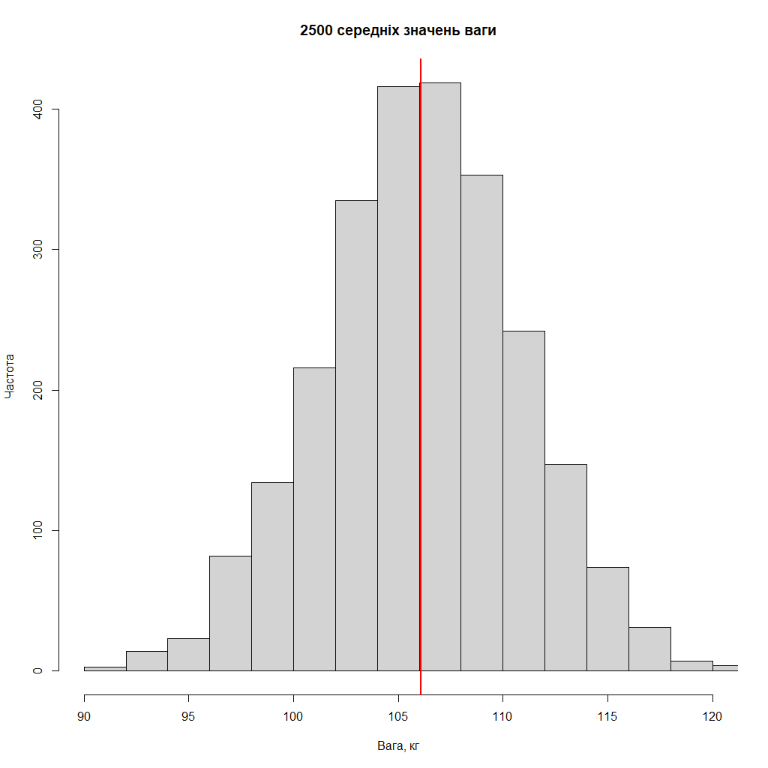
Як бачимо, чим більше вибірок однакового розміру ми робимо, тим більше розподіл середніх значень ваги гравців NBA починає нагадувати нормальний розподіл.
Відповідно, якщо ми будемо продовжимо робити вибірки, то розподіл середній значень буде все більше й більше нагадувати нормальний. Як вже було зазначено, це стосується не лише середніх значень, але й медіан, стандартних відхилень, пропорцій, розрахунків усіх можливих ratio (якщо мова йде про дві групи) і тому побідне.
Що цікаво, для того, щоб центральна гранична теорема працювала, не обов'язково, щоб популяція, з якої ми робимо вибірку, мала нормальний розподіл. Ще раз подивіться на гістограму розподілу ваги всіх гравців NBA – хоча вона й нагадує нормальну, все ж таки спостерігається пік в районі 100 кг, який зникає, коли ми починаємо робити вибірки й рахувати середню вагу.
Це означає, що маючи лише одну вибірку (як зазвичай і трапляється в медичних дослідженнях) ми можемо робити припущення про значення цілої популяції! Адже, теотерично, якщо ми будемо знову й знову робити вибірку однакового розміру, то зрештою показники, які ми розраховуємо (наприклад, середня вага), будуть мати нормальний розподіл. А однієї з властивостей нормального розподілу є те, що 95% значень в нормальному розподілі лежать в межах 2 (зовсім точно, то 1.96) стандартних похибок (якщо дуже коротко, то стандартна похибка – то це міра варіативності чисел в сукупності).
Таким чином, пройшовши відстань у дві стандартні похибки вперед і назад від отриманого значення для вибірки, ми у 95% випадків натрапимо на середнє значення для популяції – що ми і зробили вище у прикладі з Risk Ratio:
RR(жінки/чоловіки) = 0.55 (95% ДІ від 0.48 до 0.67)
Значення 0.48 лежить у межах мінус двох стандартних похибок від 0.55, а 0.67 в межах плюс двох стандарних похибок. Тож, згідно з властивостями нормального розподілу, існує вірогідність, що наш інтервал попав у 95% інтервалів з істинним значенням. Однак, також існує вірогідність, хоча й значно менша, що він попав у 5% інтервалів, до складу яких середнє значення не входить.
Також на основі центральної граничної теореми пояснюється й значення p. Фактично, значення p відображає, як далеко отриманий з вибірки результат лежить від нульового значення (значення, коли різниці між двома групами немає). Якщо значення p<0.05 -- результат лежить далі, ніж дві стандартні похибки від 0 (згідно з властивостями нормального розподілу), отже, результат є статистично значущим і отриманий не випадково.
Отакий він світ біостатистики. Можливо, нам навіть вдалося запалити у вас той вогник, який підштовхне вас до подальшого вивчення біостатистики та сподіваємось, що після прочитання обох статей у вас сформувався той фундамент, який допоможе вам розуміти наукові публікації, інтерпретувати результати досліджень та почуватись впевнено й не потонути у світі мільйонів статей, кількість яких з кожним днем зростає.
Громадська організація INgenius – україномовна медична платформа, що пропагує доказову медицину серед спільноти лікарів в Україні з 2016 року. Наша команда створила відкриту базу з перекладених протоколів лікування, аналітичних статей про достовірні методи лікування та розбори фуфломіцинів. Також ми організовуємо на високому рівні події для медиків.
Якщо Ви хочете ще більше доказового україномовного контенту, цікавіших експериментів та практичних заходів, підтримайте нас за допомогою донатів!
Зібрані кошти будуть витрачені на:
- технічне забезпечення сайту;
- щомісячний платіж за платформи такі як ZOOM, telegram і т.д.;
- оплату дизайнера;
- безкоштовні заходи;
- рекламу.
Кожний Ваш внесок - це вклад у майбутнє не тільки наше як платформи, але й також у прогресивний розвиток доказової медицини в України.
Revolution in you!
Кожний Ваш внесок - це вклад у майбутнє не тільки наше як платформи, але й також у прогресивний розвиток доказової медицини в України.
Revolution in you!

info@ingeniusua.org


